مشاوره: درخواست راهنمایی برای حل یک مشکل ریاضی در طراحی بازی (حل شد)
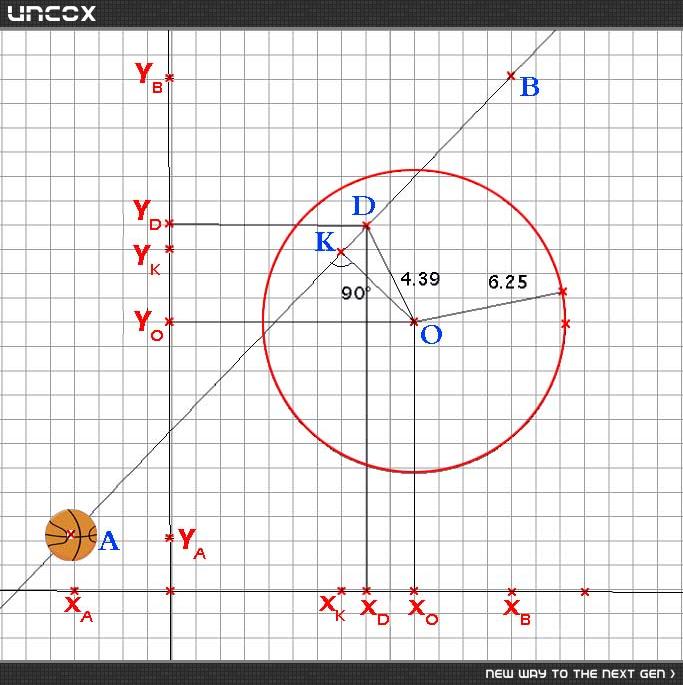
طرح مسئله:
- معلومات مسئله:
- محل نقطه B به دلخواه انتخاب كاربر است. ولي با كليك كاربر مختصاتش را داريم.
- محل نقطه Aهم محل قرارگيري مثلا يك توپ است كه مختصات آن را هم داريم.
- يك توپ ديگر هم داريم كه در مركز O قرار دارد و به شعاع r است كه اينها هم مشخص است. (اين توپ كه به رنگ قرمز است را از قصد بزرگ كشيده ام براي انجام محاسبات هندسي).
- سوال اصلي مسئله:
- كاربر هرجا كه كليك كند توپ به آن نقطه منتقل ميشود (يعني نقطه B) ولي اگر در مسير حركت توپ A ، توپ ديگري قرار داشته باشد (مثل توپ O) توپ اجازه حركت ندارد. بايد الگوريتمي را براي تشخيص اينكه در مسير توپ A توپ ديگري نيز قرار دارد يا نه بدست بياوريم.
نتايجي رو كه تا الان بدست آوردم در ادامه همين تاپيك در يك پاسخ جداگانه مي نويسم كه مشخص باشه. فعلا به دو نتيجه رسيدم. يكي راهي كه دوست عزيز Almassi پيشنهاد كرده كه نياز به محاسبات رياضي روي كاغذ خيلي زياد و پيچيده اي داره كه در نهايت به يك فرمول دست پيدا كني كه در ادامه ميارم (راستش در مورد اول مخم واقعا هنگ كرد و ننونستم به محاسبات ادامه بدم برا همين رفتم سراغ راه حل دوم) و روش دوم كه خودم بهش رسيدم كه راه خيلي ساده تري هست ولي پردازش CPU بيشتري رو مي طلبه. خوشحال ميشم كه دوستان نظرشون رو بيان كنند. و اگه راه ديگه اي هم به ذهنشون مي رسه بگن.
گزارش نتيجه راه حل دوم:
كمي كه به شكل دقت كردم به اين فكر رسيدم كه به جاي تمركز روي نطقه K ، روي نقطه D كه روي هر جايي از خط AB مي تونه باشه تمركز كنم و ديدم كه اين نقطه با نطقه O يه مثلث قائم الزاويه مي سازه كه قضيه فيثاغورث توش برقراره:
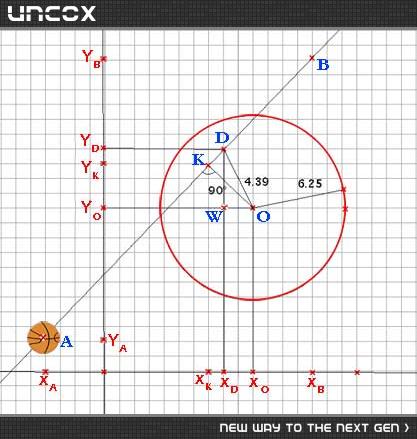
در مثلت قائم الزاويه WDO هميشه رابطه فيثاغورث برقراره يعني:
WO^2+WD^2=OD^2
OD<r خط داخل دايره است.
OD=r خط مماس دايره است.
OD>r خط بيرون دايره است.
از طرفي نقطه W مختصاتش براحتي قابل محاسبه است و فرمول ساده زير براحتي بدست مياد:
(Xo-Xd)^2+(Yo-Yd)^2<r^2
و چون نقطه D نقطه ثابتي نيست و منظور تمامي نقاط روي خط AB هست پس مي شود x , y كه در معادله خط AB صدق ميكنه.
تنها كاري كه بايد كرد اين است كه بطور دائم در يك حلقه for تمامي نقاط روي خط AB شرط صدق بودن نامساوي بالا براشون چك بشه كه معلوم بشه آيا خط با دايره تقاطع داره يا نه و اين كار بطور دائم بايد انجام بشه چون نقطه B هم نقطه اتنخابي كاربر هست و اون هم دائم در حال تغيير هست. تنها نكته اي كه باقي ميمونه اينه كه آيا سرعت پردازش آنقدر بالا هست كه اين محاسبات رو بطور آني انجام بده و بازي كند نشه؟
بي صبرانه منتظر نظر دوستان عزيز و گرامي هستم كه اگه راهنمايي به ذهنشون ميرسه بگن.
با سلام. به کمک دوست خوبم جناب Almassi و تابعی که برام فرستادند کلا مشکلم حل شد. نه راه حل اولم درست بود و نه راه حل دومم.
راه حل دوم به دلیل بار پردازشی زیادی که روی CPU میگذاره رد شده و راه حل اولم هم بدلیل محاسبات ریاضی بی دلیل و اضافی رد شده. اینجاست که انتخاب الگوریتم مناسب خودش رو با قدرت هرچه تمام تر به رخ میکشه. و اما تابع طلایی:
public int calc(double x1, double y1, double x2, double y2, double xo, double yo, double r) {
double dx, dy;
double a, b; ////y=ax+b
double x, y;
boolean isxok = false;
boolean isyok = false;
if (y2 == y1) {
y1 += 0.000001;
}
if (x2 == x1) {
x1 += 0.000001;
}
////// به میزان 0.0000001 در مختضات در صورت تساوی اضافه میشود که تقسیم بر صفر نداشته باشیم - خطای چندانی هم ایجاد نمی کنه
dx = (x2 - x1);
dy = (y2 - y1);
a = dy / dx;
b = y2 - a * x2;
////////////// معادله خط اول حساب شد
double A, B;
A = -1 / a;
B = yo - A * xo;
/// معادله پاره خط عمودی بر ab بدست آمد
x = (B - b) / (a - A);
y = A * x + B;
////// مختصات محل تقاطع بدست آمد
if (x2 > x1) {
if (x > x1 && x < x2) {
isxok = true;
}
} else {
if (x > x2 && x < x1) {
isxok = true;
}
}
if (y2 > y1) {
if (y > y1 && y < y2) {
isyok = true;
}
} else {
if (y > y2 && y < y1) {
isyok = true;
}
}
////کنترل وقوع نقطه تقاطع بر روی پاره خط
if (isxok && isyok) {
double dist;
dist = Math.sqrt(Math.pow((xo - x), 2) + Math.pow((yo - y), 2));
if (dist == r) {
return 0; //// وقتی مماس است
}
else if (dist < r) {
return 1; /// وقتی تقاطع دارد
}
else if (dist > r) {
return -1; /// وقتی که تقاطع ندارد
}
} else {
return -1;
}
return -1;
}
ببینید که با چه روش ساده ای معادله خط محاسبه شده و همچنین محل تقاطع خطوط. از همین معادله استفاده کردم و تابع محاسبه شوت توپ به سمت دروازه و چک کردن اینکه آیا گل شده یا نه رو بدست آوردم که اگه دوست داشتید اون رو هم می زارم. اگه به توضیح بیشتری نیاز بود بگید تا بگم.
اینجوریه که یه برنامه نویس در کارهای عملی و تجربی درسهای جدید یاد میگیره که پای درس هیچ استادی نمیتونه اون نکات رو یاد بگیره. بازم دم این انجمن و بچه های گلش گرم که به بقیه دوستای انجمن کمک میکنن. ممنون جناب Almassi !
دوستان از این مثال و کاربرد ریاضی در برنامه نویسی بازی خیلی میتونید استفاده کنید. از اول تا آخر کار رو بررسی کنید و ببنید که چرا من روش اشتباهی رو برای ورود به مسئله انتخاب کرده بودم، و ببینید که در بیشتر حالتها چیزهای به ظاهر پیچیده چقدر راه حل ساده ای میتونند داشته باشند.
یه سوال که بی ربط به این موضوع نیست..
چطور میشه مختصات x و y رو خودمون بدیم و مقداردهی کنیم.???
البته به وسیله کلاس onTouch و رویداد Event!!!
پاسخگویی و مشاهده پاسخ های این سوال تنها برای اعضای ویژه سایت امکان پذیر است .
چنانچه تمایل دارید به همه بخش ها دسترسی داشته باشید میتوانید از این بخش لایسنس این آموزش را خریداری نمایید .




